How to Implement a Decision Tree Algorithm in Python

Decision Trees are one of the most popular machine learning algorithms because they are easy to understand compared to more complex algorithms like Neural Networks. In this example we will look at a classification problem using the well-known Iris dataset.

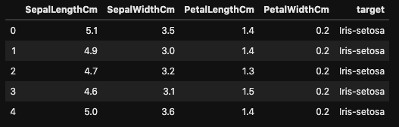
The dataset has feature columns that describe each type of flower in the target column. The features include sepal length, sepal width, petal length and petal width. The types of flowers include an even number of Iris-setosa, Iris-versicolor, and Iris-virginica.

Begin with the baseline

In any machine learning task, we want to beat the baseline. In a classification problem, the baseline would be to guess the majority class every time resulting in a 33.33% accuracy score since each flower is 1/3 of the dataset. That accuracy score is very low and I bet we can improve the score by a lot using decision trees.

How does it work?

The decision tree is trained on a dataset with features and a target column. The algorithm learns patterns in the features that map to the target that it is able to use to predict on new flowers using unseen features.

First, we need to split the dataset into a training dataset and a testing dataset. The training dataset is what the algorithm learns from and the testing dataset is what the algorithm is tested on to see how it applies its learning to new information.

# train test split
def train_test_split(df, target, test_size):
    # shuffles data
    random_df = df.sample(frac=1)
    # splits data into train and test based on test size %
    test_split = int(test_size * len(df))
    train_df = random_df[test_split:]
    test_df = random_df[:test_split]
    return train_df, test_df
    
train_df, test_df = train_test_split(df, target='label', test_size=.2)
# check to see that data is split properly
train_df.shape, test_df.shape

A tree starts with a root node, which asks a question of an attribute. If data is pure, meaning the data split on that attribute is of all one class, the answer to the question is yes. If the data is pure the tree has reached a leaf or terminal node and a classification is made. If the data is impure, meaning there are multiple classes with that attribute, the answer to the question is no. The tree grows, continuing to split on different attributes until all splits are pure, leaf nodes are reached and classifications are made.

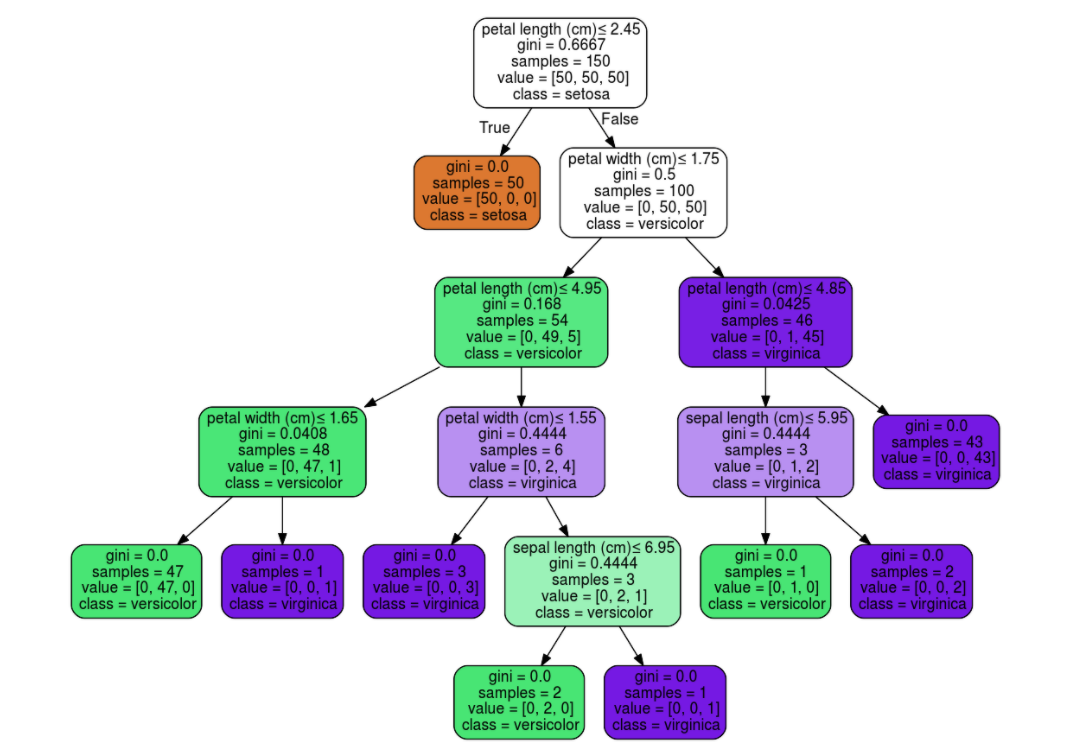
How does the algorithm know which attributes to split on? Using Entropy and Information Gain! Entropy is a measure of purity that ranges from 0 to 1, with 0 being pure or containing 1 class and 1 being impure containing none of that particular class. In the decision tree above the measure of impurity used is called “gini”, but it’s still the same idea. As you can see, when a leaf node has been reached, the gini = 0.0.

    def calculate_entropy(self, data):
        # access all the rows of the target column of the data
        target_column = data[:, -1]
        # determine the number of unique classes
        _, counts = np.unique(target_column, return_counts=True)
        # get probabilites of each class
        probabilities = counts / counts.sum()
        entropy = sum(probabilities * -np.log2(probabilities))
        return entropy

    def info_gain(self, data, column_index, splitval):
        split_column_values = data[:, column_index]
        data_left = data[split_column_values <= splitval]
        data_right = data[split_column_values > splitval]

        data_points = len(data_left) + len(data_right)
        p_data_left = len(data_left) / data_points
        p_data_right = len(data_right) / data_points

        info_gain = self.calculate_entropy(data) - (p_data_right * self.calculate_entropy(data_right) 
                    + p_data_left *  self.calculate_entropy(data_left))
        return info_gain

After the dataset is split on an attribute, the entropy for the left and right branches is calculated. The entropies are summed and then subtracted from the entropy before the split. The result is the Information Gain or decrease in entropy. The dataset is split on the attribute that returns the highest information gain.

    def find_best_split(self, data):
        bestgain = 0
        _, n_columns = data.shape
        for column_index in range(n_columns-1):
            values = data[:, column_index]
            unique_values = np.unique(values)
            for i in range(1,len(unique_values)):
                splitval = (unique_values[i-1] + unique_values[i]) / 2
                gain = self.info_gain(data, column_index, splitval)
                if gain >= bestgain:
                    bestgain = gain
                    bestattr = column_index
                    bestsplitval = splitval
        return bestattr, bestsplitval

Once the tree has been constructed from the training data, we can use it to test on unseen flowers.

By calling the predict method new features traverse the tree until they reach a classification. The predicted classification is then compared to the actual classification and an accuracy score is calculated.

We can now compare our accuracy score to the baseline of 33% and to the scikit-learn DecisionTreeClassifier score.

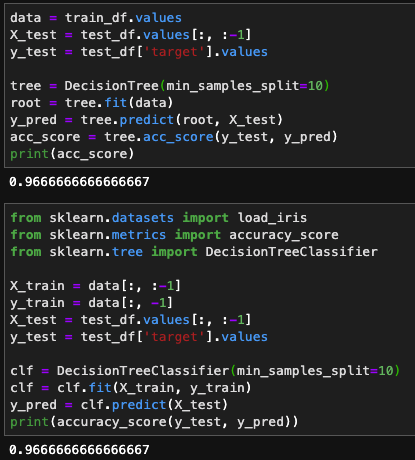
You can view the full code here.